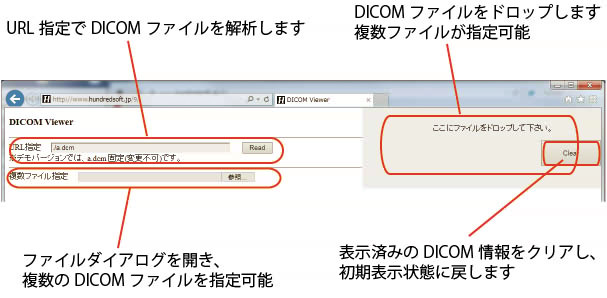
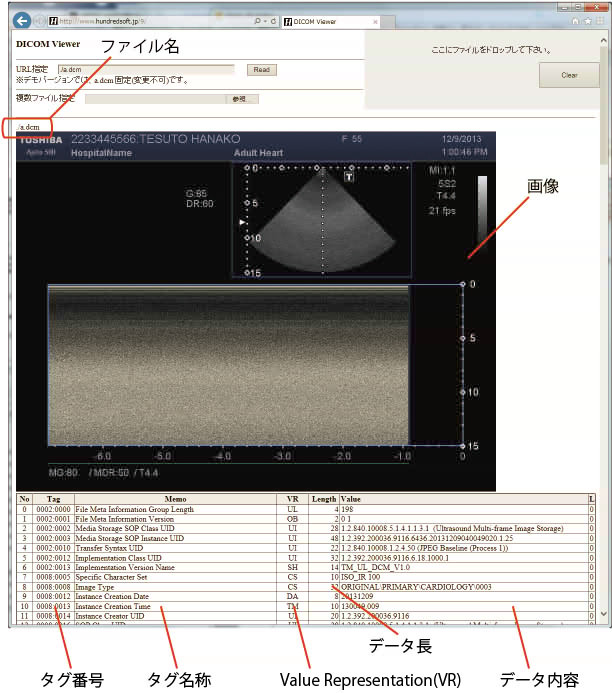
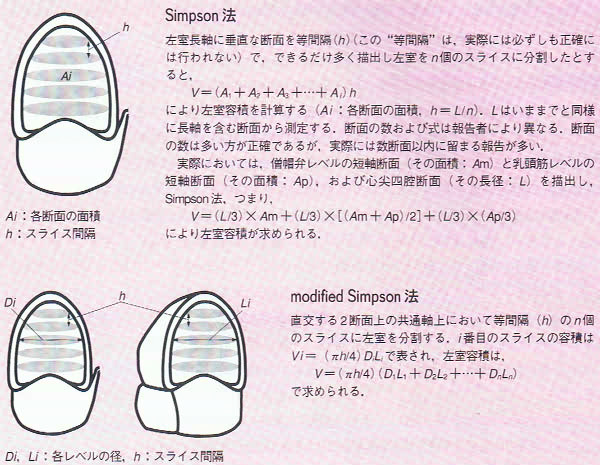
Echoを使った左室容積の計算方法には幾つかあるのですが、4腔断面・2腔断面の両方が得られる場合に、良く使われるのが Modified Simpson法です。
日本医師会雑誌の「心エコーのABC」から計算部分を抜粋。
一見、簡単なプログラムで構築できそうですが、交点算出が割と面倒です。
ここでは、javascriptでの実装を目指します。
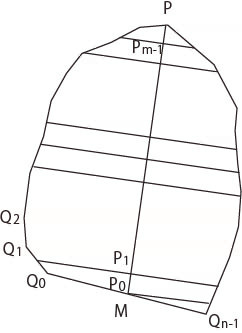
トレースラインを Q0, Q1, Q2, ...で表し、その長径をMPで表す。
MPをm分割し、分割点をP0, P1, P2, ... とする。
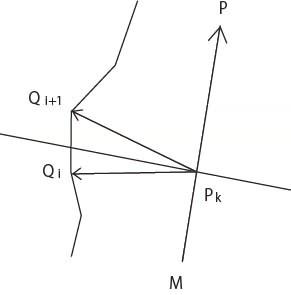
等間隔で分割することにして、k番目の分割線の垂線が、トレース座標のQi, Qi+1線分を横切ることを考える。
直線MPと 直線(Pk)-(Qi)のベクトル内積は負になるが、MPと (Pk)-(Qi+1)のベクトル内積は正になる。
内積符号が異なった場合に、各トレース座標間の直線(Q)と分割点(Pk)からのMPの直交ベクトルとの交点が、候補になる。
トレースラインが捻じれる場合もあるので、分割点(Pk)から最も遠い候補を解とする。
また、左右それぞれに解を求める必要があるので、MPと分割点(Pk)から解までのベクトルとで、
外積を取り、左右どちらの解であるかを確認する。
複雑そうに思えるかもしれないが、ループ回数は、トレースポイント数 x 分割数 でしかなく、
四則演算だけでコードが書ける。
この解説部分に該当する関数名は、calc() で、 85行しかない。

デモプログラムでは、実運用に近づけるため、B-DUAL画像を模して左右に、4腔断面と2腔断面を配置し、
下段に、Modified Simponによる体積を表示する。
左右画像上に表示されるSimpson値は、単画像による等分割で、回転体により体積を求めた場合の数値で、
最初に載せた文献によれば、これを計測値とすることは少ないようです。
ここでは、アルゴリズムの紹介であるので、[pix]単位の計算結果を表示している。
生体長換算値 [cm/pix]があれば、生体長換算値を3回掛ければ [mL] での結果が求まる。
Canvasは、左右と下段の3枚を使っている。
スライス算出部は、2つnewして、左右それぞれに振り、
結果が求まった時点で、callbackにより、下段のスクリプトを呼び出す仕組みにした。
実行サンプルはこちら
Chrome, FF, IE11 で動作確認しています。
以下はソースコードです。
html と js の各1本です。
[html]
<!DOCTYPE html>
<html>
<head>
<meta http-equiv="Content-Type" content="text/html; charset=utf-8" />
<meta http-equiv="X-UA-Compatible" content="IE=edge" />
<meta name="viewport" content="width=device-width, initial-scale=1.0, user-scalable=no" />
<title>Modified Simpson</title>
<style type="text/css">
#div1 {
width:800px;
height:600px;
}
#canvas1 {
width:400px;
height:500px;
background-color:#f0f0e0;
float:left;
}
#canvas2 {
width:400px;
height:500px;
background-color:#e0f0f0;
float:left;
}
#canvas3 {
width:800px;
height:100px;
background-color:#f0e0f0;
float:left;
clear: both;
}
</style>
<script type="text/javascript" src="DSM.js"></script>
<script type="text/javascript">
var init = function(){
ModifiedSimpson.init(document.getElementById("canvas3"), 20);
var dsm1 = new DSMPublic.DSM(document.getElementById("canvas1"),
function(hd){
ModifiedSimpson.paint(1, hd);
});
var dsm2 = new DSMPublic.DSM(document.getElementById("canvas2"),
function(hd){
ModifiedSimpson.paint(2, hd);
});
};
</script>
</head>
<body onload="init();">
Modified Simpson's Rule Sample<br /><br />
<div id="div1">
<canvas id="canvas1" width="400" height="500"></canvas>
<canvas id="canvas2" width="400" height="500"></canvas>
<canvas id="canvas3" width="800" height="100"></canvas>
</div>
</body>
</html>
[js]
// (c)Hundredsoft Corporation. 2015 All right reserved.
// NAME
// DSM.js
//
// FUNCTION
// Modified Simpson's rule.
//
// REVISION
// 1.00 T.Furumoto Jan-30-2015 Original
//
// UTF-8で保存して下さい
//
////////////////////////////////////////////////////////////
new function() {
///////////////////////////////////
// Private Scope
///////////////////////////////////
var m_linesz = 1;
var m_Slice = 20;
var m_Chain = 2;
var mdown = function(p, mouseX, mouseY){
if (p.m_mode != 1){
clear(p);
}
};
var mup = function(p, mouseX, mouseY){
var ret;
if (p.m_mode == 0){
p.m_trace = traceChain(p.m_trace);
p.m_P = autoL(p.m_trace);
ret = calc(p.m_trace, p.m_P);
if (ret){
paint(p, ret);
p.m_mode = 1;
}else{
errorDisp(p);
}
}else if (p.m_mode == 1){
p.m_mode = 0;
ret = calc(p.m_trace, p.m_P);
if (ret){
paint(p, ret);
}else{
errorDisp(p);
}
}
};
var mmove = function(p, mouseX, mouseY){
if (p.m_mode == 0){
var n = p.m_trace.x.length;
p.m_trace.x[n] = mouseX;
p.m_trace.y[n] = mouseY;
drawROI(p);
}else{
p.m_P = manualL(p.m_trace, mouseX, mouseY);
var ret = calc(p.m_trace, p.m_P);
if (ret){
paint(p, ret);
}else{
errorDisp(p);
}
}
};
var intersection = function(p1x, p1y, p2x, p2y, q1x, q1y, q2x, q2y){
var a = p1y - p2y;
var b = -p1x + p2x;
var c = q1y - q2y;
var d = -q1x + q2x;
var det = a*d - b*c;
if( det * det < 0.01 ) // 平行
return false;
var e = a * p1x + b * p1y;
var f = c * q1x + d * q1y;
return {"x" : (d*e - b*f) / det, "y" : (-c*e + a*f) / det};
};
var autoL = function(trace){
var n = trace.x.length;
var mx = (trace.x[n-1] + trace.x[0]) / 2;
var my = (trace.y[n-1] + trace.y[0]) / 2;
var len2 = 0;
var px = false;
var py = false;
for (var i=0; i<n; i++){
var w = (mx - trace.x[i]) * (mx - trace.x[i])
+ (my - trace.y[i]) * (my - trace.y[i]);
if (w > len2){
len2 = w;
px = trace.x[i];
py = trace.y[i];
}
}
return {"x": px, "y": py};
};
var manualL = function(trace, mouseX, mouseY){
var n = trace.x.length;
// Pointから最も近い点(p)
var px = trace.x[0];
var py = trace.y[0];
var lmin = (px - mouseX) * (px - mouseX) + (py - mouseY) * (py - mouseY);
for( var i=1; i<n; i++ ){
var l = (trace.x[i] - mouseX) * (trace.x[i] - mouseX)
+ (trace.y[i] - mouseY) * (trace.y[i] - mouseY);
if( l < lmin ){
px = trace.x[i];
py = trace.y[i];
lmin = l;
}
}
return {"x": px, "y": py};
};
var traceChain = function(o_trace){
var n = o_trace.x.length;
var traceX = [];
var traceY = [];
traceX.push(o_trace.x[0]);
traceY.push(o_trace.y[0]);
for (var i=1; i<n; i++){
var dx = o_trace.x[i] - o_trace.x[i-1];
var dy = o_trace.y[i] - o_trace.y[i-1];
var len = dx * dx + dy * dy;
if (len > m_Chain * m_Chain * m_Chain * m_Chain){
var m = ~~(Math.sqrt(len) / m_Chain);
var ex = dx / m;
var ey = dy / m;
var x = o_trace.x[i-1] + ex;
var y = o_trace.y[i-1] + ey;
for (var j=1; j<m-1; j++){
traceX.push(x);
traceY.push(y);
x += ex;
y += ey;
}
}
traceX.push(o_trace.x[i]);
traceY.push(o_trace.y[i]);
}
return {"x": traceX, "y": traceY};
};
var calc = function(trace, p){
var n = trace.x.length;
if (n < m_Slice * 2 + 2){
return false;
}
var mx = (trace.x[n-1] + trace.x[0]) / 2;
var my = (trace.y[n-1] + trace.y[0]) / 2;
// M-Pベクトル
var lx = p.x - mx;
var ly = p.y - my;
// M-Pに直行するベクトル
var vx = ly;
var vy = -lx;
var out_plx = [];
var out_ply = [];
var rlen = [];
var llen = [];
for( var i=0; i<m_Slice+1; i++ ){
rlen[i] = -9999999999;
llen[i] = 9999999999;
}
var qox = mx;
var qoy = my;
for (var i=0; i<n+1; i++){
var qnx = mx;
var qny = my;
if( i != n ){
qnx = trace.x[i];
qny = trace.y[i];
}
for (var j=0; j<m_Slice+1; j++){
var px = (mx * (m_Slice-j) + p.x * j) / m_Slice;
var py = (my * (m_Slice-j) + p.y * j) / m_Slice;
// 線をまたぐか?
if( ( (qox - px) * lx >= -(qoy - py) * ly
&& (qnx - px) * lx < -(qny - py) * ly )
|| ( (qox - px) * lx < -(qoy - py) * ly
&& (qnx - px) * lx >= -(qny - py) * ly ) )
{
// 交点座標
var t = intersection(qox, qoy, qnx, qny, px, py, px+vx, py+vy);
if (!t){
var d1x = qnx - px;
var d1y = qny - py;
var d2x = qox - px;
var d2y = qoy - py;
if( (d1x * d1x + d1y * d1y) > (d2x * d2x + d2y * d2y) ){
t = {"x" : qnx, "y" : qny};
}else{
t = {"x" : qox, "y" : qoy};
}
}
var qtlen = (t.x-px) * (t.x-px) + (t.y-py) * (t.y-py);
// 方向確認
if( (t.x - px) * vx + (t.y - py) * vy > 0 ){
qtlen *= -1.;
}
// 最遠方点なら更新
if( qtlen < llen[j] ){
out_plx[j*2] = t.x;
out_ply[j*2] = t.y;
llen[j] = qtlen;
}
if( qtlen > rlen[j] ){
out_plx[j*2+1] = t.x;
out_ply[j*2+1] = t.y;
rlen[j] = qtlen;
}
}
}
qox = qnx;
qoy = qny;
}
return {"x": out_plx, "y": out_ply};
};
var clear = function(p){
m_Slice = ModifiedSimpson.getSlice();
p.m_trace.x = [];
p.m_trace.y = [];
p.m_ctx.font = "16px 'MS Gothic'";
p.m_mode = 0;
p.m_ctx.clearRect(0, 0, p.m_width, p.m_height);
p.callback({"H":0, "D":false});
};
var drawROI = function(p){
var ctx = p.m_ctx;
ctx.clearRect(0, 0, p.m_width, p.m_height);
ctx.beginPath();
ctx.arc(p.m_trace.x[0], p.m_trace.y[0], m_linesz, 0, Math.PI*2, false);
ctx.fill();
ctx.closePath();
var n = p.m_trace.x.length;
for (var i=1; i<n+1; i++){
ctx.beginPath();
ctx.arc(p.m_trace.x[i], p.m_trace.y[i], m_linesz, 0, Math.PI*2, false);
ctx.fill();
ctx.closePath();
ctx.lineWidth = m_linesz * 2;
ctx.strokeStyle = "#808000";
ctx.beginPath();
ctx.moveTo(p.m_trace.x[i-1], p.m_trace.y[i-1]);
ctx.lineTo(p.m_trace.x[i], p.m_trace.y[i]);
ctx.stroke();
ctx.closePath();
}
};
var paint = function(p, out_pl){
drawROI(p);
var ctx = p.m_ctx;
var n = p.m_trace.x.length;
var mx = (p.m_trace.x[n-1] + p.m_trace.x[0]) / 2;
var my = (p.m_trace.y[n-1] + p.m_trace.y[0]) / 2;
ctx.lineWidth = m_linesz * 2;
ctx.strokeStyle = "#808000";
ctx.beginPath();
ctx.moveTo(p.m_trace.x[0], p.m_trace.y[0]);
ctx.lineTo(p.m_trace.x[n-1], p.m_trace.y[n-1]);
ctx.stroke();
ctx.moveTo(mx, my);
ctx.lineTo(p.m_P.x, p.m_P.y);
ctx.stroke();
ctx.closePath();
// M-Pベクトル
var lx = p.m_P.x - mx;
var ly = p.m_P.y - my;
var leng = Math.sqrt(lx*lx + ly*ly);
var area = 0;
for (var i=0; i<n; i++){
var j = (i == n-1) ? 0 : i+1;
area += p.m_trace.x[i] * p.m_trace.y[j] - p.m_trace.x[j] * p.m_trace.y[i];
}
area = Math.abs(area);
var v = 0;
var h = leng / m_Slice;
var d2 = [];
var hpi = Math.PI * h / 4.0;
for (var i=0; i<m_Slice+1; i++){
if (i < m_Slice){
var dx = out_pl.x[i*2+1] - out_pl.x[i*2 ];
var dy = out_pl.y[i*2+1] - out_pl.y[i*2 ];
var d = (dx*dx + dy*dy);
d2.push(d);
v += hpi * d;
}
ctx.beginPath();
ctx.moveTo(out_pl.x[i*2 ], out_pl.y[i*2 ]);
ctx.lineTo(out_pl.x[i*2+1], out_pl.y[i*2+1]);
ctx.stroke();
ctx.closePath();
}
ctx.fillText("Simpson: " + Math.round(v) + " [pix^3]", 20, 20);
ctx.fillText("Area: " + Math.round(area) + " [pix^2]", 20, 40);
ctx.fillText("L: " + Math.round(leng) + " [pix]", 20, 60);
p.callback({"H":h, "D":d2});
};
var errorDisp = function(p){
var ctx = p.m_ctx;
var n = p.m_trace.x.length;
ctx.beginPath();
ctx.moveTo(p.m_trace.x[0], p.m_trace.y[0]);
ctx.lineTo(p.m_trace.x[n-1], p.m_trace.y[n-1]);
ctx.stroke();
ctx.closePath();
ctx.fillText("トレースラインが短すぎます", 20, 50);
};
///////////////////////////////////
// Public Scope
///////////////////////////////////
DSMPublic = {
DSM: function(canvas, callback){
this.m_ctx = null;
this.m_width = 400;
this.m_height = 400;
this.m_trace = {"x": [], "y": []};
this.m_mode = 0;
this.m_P = {"x": 0, "y": 0};
this.callback = callback;
var iam = this;
var mouseDown = false;
var mouseX = 0;
var mouseY = 0;
if (navigator.userAgent.indexOf('iPhone')>0 ||
navigator.userAgent.indexOf('iPod')>0 ||
navigator.userAgent.indexOf('iPad')>0 ||
navigator.userAgent.indexOf('Android')>0) {
canvas.addEventListener('touchstart',
function(e) {
e.preventDefault();
var n = e.touches.length;
if (n > 0) {
e = e || window.event;
mouseDown = true;
var rect=e.target.getBoundingClientRect();
mouseX = e.touches[n-1].pageX-rect.left;
mouseY = e.touches[n-1].pageY-rect.top;
mdown(iam, mouseX, mouseY);
}
}, false);
canvas.addEventListener('touchend',
function(e) {
mouseDown = false;
mup(iam, mouseX, mouseY);
}, false);
canvas.addEventListener('touchmove',
function (e) {
e.preventDefault();
var rect=e.target.getBoundingClientRect();
var n = e.touches.length;
if (n > 0){
mouseX = e.touches[n-1].pageX-rect.left;
mouseY = e.touches[n-1].pageY-rect.top;
if (mouseDown) {
mmove(iam, mouseX, mouseY);
}
}
}, false
);
}else{
canvas.addEventListener('mousedown',
function(e) {
e.preventDefault();
mouseDown = true;
e = e || window.event;
var rect=e.target.getBoundingClientRect();
mouseX = e.clientX-rect.left;
mouseY = e.clientY-rect.top;
mdown(iam, mouseX, mouseY);
}, false);
canvas.addEventListener('mouseup',
function(e) {
mouseDown = false;
mup(iam, mouseX, mouseY);
}, false);
canvas.addEventListener('mousemove',
function (e) {
e.preventDefault();
var rect=e.target.getBoundingClientRect();
mouseX = e.clientX-rect.left;
mouseY = e.clientY-rect.top;
if (mouseDown) {
mmove(iam, mouseX, mouseY);
}
}, false
);
}
this.m_ctx = canvas.getContext('2d');
this.m_width = canvas.width;
this.m_height = canvas.height;
clear(this);
}
} // Public Scope
}; // Constructor
///////////////////////////////////
//
// Measurement Display Area
//
///////////////////////////////////
new function() {
///////////////////////////////////
// Private Scope
///////////////////////////////////
var m_ctx = null;
var m_width = 100;
var m_height = 100;
var m_m1 = {"H": 0, "D": false};
var m_m2 = {"H": 0, "D": false};
var m_Slice = 20;
var report = function(){
if (!m_ctx){
return;
}
m_ctx.clearRect(0, 0, m_width, m_height);
if (m_m1.D && m_m2.D){
var h = (m_m1.H + m_m2.H) / 2;
var v = 0;
var hpi = Math.PI * h / 4.0;
for (var i=0; i<m_Slice; i++){
v += hpi * Math.sqrt( m_m1.D[i] * m_m2.D[i] );
}
m_ctx.fillText("Modified Simpson: " + Math.round(v) + " [pix^3]", 50, 50);
}
};
///////////////////////////////////
// Public Scope
///////////////////////////////////
ModifiedSimpson = {
init: function(canvas, slc){
if (slc){
m_Slice = slc;
}
m_ctx = canvas.getContext('2d');
m_width = canvas.width;
m_height = canvas.height;
m_ctx.font = "16px 'MS Gothic'";
m_ctx.clearRect(0, 0, m_width, m_height);
},
paint: function(id, hd){
if (id == 1){
m_m1 = hd;
}else if (id == 2){
m_m2 = hd;
}
report();
},
getSlice: function(){
return m_Slice;
}
} // Public Scope
}; // Constructor
Tags:
プログラムメモ