πのBBP計算でモンゴメリを使う
| プログラムメモ | 2012/05/06 Sun 09:56
現在では10兆桁を超えるπが求められているが、πの特定の桁だけを算出する方法が知られていて、
πの部分算出の記録では500兆桁を超えている。
この部分算出の元になったのが、次の公式です。
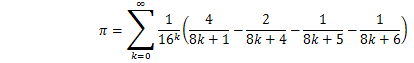
この式からd桁目を求めるために、16^dを乗じて、小数点以下を取りだすことを考える。
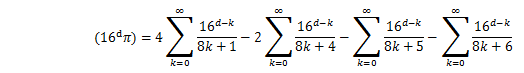
ここでSを次のように定義する。
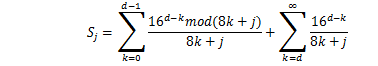
すると
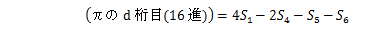
これが1995年にSimon Plouffe(プラウフ)により発見された、BBP(Bailey-Borwein-Plouffe)公式と呼ばれるもので、
これをプログラムしたものが、
http://www.experimentalmath.info/bbp-codes/ にあります。(piqpr8.c)
ここでは右向きバイナリ法を使って剰余(mod)を求めているが、剰余計算にモンゴメリ法を使うことを考える。
モンゴメリ法については過去にも
http://www.hundredsoft.jp/win7blog/log/eid93.html や
http://www.hundredsoft.jp/win7blog/log/eid98.html でサンプルを載せていますが、
高速なモンゴメリ法では、法は奇数であることが望ましい。
S1,S5の法は、8k+1,8k+5であるので奇数であるが、
S4,S6は偶数となるので、このままでは使えない
整数論の定理の中に次のものがある。
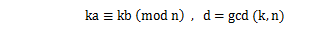 ならば
ならば
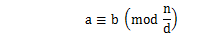
が成り立つ。
これをS4の第一項に当てはめると、
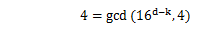
であるから、
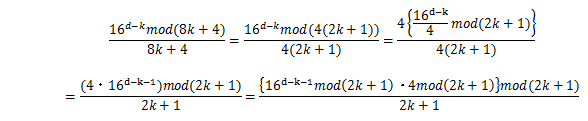
同様にS6の第一項は、
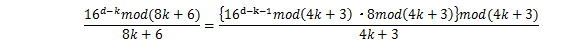
これで法が奇数となり、高速なモンゴメリ法を使うことができる。
プログラムは次のようになる。 (defaultではπの100万桁(Hex)目を算出する。)
改変は、series() のm=4,m=6の処理とexpm()→expmong()です。
intel系x86コードでの64bit整数演算は早くないので、面白い結果が出ました。
【右向きバイナリ法(WindowsXP 32bit)】
(1回目)
position = 1000000
fraction = 0.423429797567895
hex digits = 6C65E52CB4
time = 2.763[sec]
(2回目)
position = 1000000
fraction = 0.423429797567895
hex digits = 6C65E52CB4
time = 2.804[sec]
(3回目)
position = 1000000
fraction = 0.423429797567895
hex digits = 6C65E52CB4
time = 2.763[sec]
【モンゴメリ法(WindowsXP 32bit)】
(1回目)
position = 1000000
fraction = 0.423429797567801
hex digits = 6C65E52CB4
time = 3.114[sec]
(2回目)
position = 1000000
fraction = 0.423429797567801
hex digits = 6C65E52CB4
time = 3.134[sec]
(3回目)
position = 1000000
fraction = 0.423429797567801
hex digits = 6C65E52CB4
time = 3.204[sec]
【結果】
およそ15%、モンゴメリ法が時間が掛る
【右向きバイナリ法(Windows7 64bit)】
(1回目)
position = 1000000
fraction = 0.423429797567895
hex digits = 6C65E52CB4
time = 1.788[sec]
(2回目)
position = 1000000
fraction = 0.423429797567895
hex digits = 6C65E52CB4
time = 1.801[sec]
(3回目)
position = 1000000
fraction = 0.423429797567895
hex digits = 6C65E52CB4
time = 1.786[sec]
【モンゴメリ法(Windows7 64bit)】
(1回目)
position = 1000000
fraction = 0.423429797567895
hex digits = 6C65E52CB4
time = 1.255[sec]
(2回目)
position = 1000000
fraction = 0.423429797567895
hex digits = 6C65E52CB4
time = 1.258[sec]
(3回目)
position = 1000000
fraction = 0.423429797567895
hex digits = 6C65E52CB4
time = 1.223[sec]
【結果】
およそ30%、モンゴメリ法が早い
VC2010でBuildした限りでは、
32bitではバイナリ法の方が早く、64bitではモンゴメリ法の方が早くなりました。
バイナリ法のコードも整数演算化してみたのですが、
部分的なコード変更だと、かえって成績が悪くなってしまいました。
バイナリ法のコンパイラオプションでSSE2を有効にしてみてもあまり効果はなかったのですが、
Intelコンパイラを使うと、もう少し早くなるかもしれません。
このコードでも、2〜3千万桁までは計算できますが、
expmong()の変数 r2 と series()の変数 p の型を__int64にすれば、1億桁まで計算できるようになります。
但し、x86(32bit)だと64bit整数演算が増えるとそれだけ処理が遅くなります。
x64で1億桁の計算は、私のPCでは150秒ほどでした。
拡張倍精度(仮数部64bit)と長整数(80bit程度)を組み合わせれば、このアルゴリズムでも100億桁ぐらいは行けると思いますが、これだけの計算量になると普通のPCでは難しいです。(電気代も上がるし...)
Tags: プログラムメモ
πの部分算出の記録では500兆桁を超えている。
この部分算出の元になったのが、次の公式です。
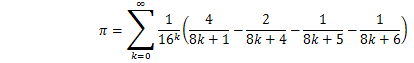
この式からd桁目を求めるために、16^dを乗じて、小数点以下を取りだすことを考える。
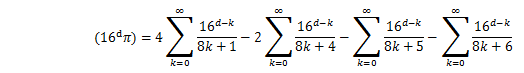
ここでSを次のように定義する。
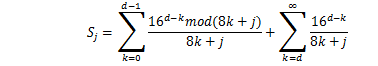
すると
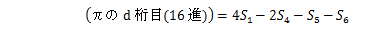
これが1995年にSimon Plouffe(プラウフ)により発見された、BBP(Bailey-Borwein-Plouffe)公式と呼ばれるもので、
これをプログラムしたものが、
http://www.experimentalmath.info/bbp-codes/ にあります。(piqpr8.c)
ここでは右向きバイナリ法を使って剰余(mod)を求めているが、剰余計算にモンゴメリ法を使うことを考える。
モンゴメリ法については過去にも
http://www.hundredsoft.jp/win7blog/log/eid93.html や
http://www.hundredsoft.jp/win7blog/log/eid98.html でサンプルを載せていますが、
高速なモンゴメリ法では、法は奇数であることが望ましい。
S1,S5の法は、8k+1,8k+5であるので奇数であるが、
S4,S6は偶数となるので、このままでは使えない
整数論の定理の中に次のものがある。
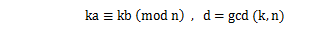 ならば
ならば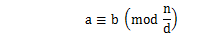
が成り立つ。
これをS4の第一項に当てはめると、
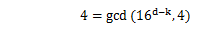
であるから、
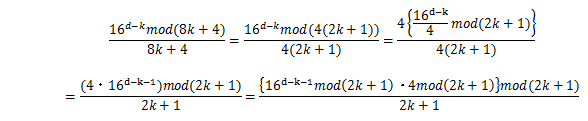
同様にS6の第一項は、
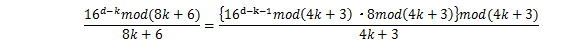
これで法が奇数となり、高速なモンゴメリ法を使うことができる。
プログラムは次のようになる。 (defaultではπの100万桁(Hex)目を算出する。)
#include <stdio.h> #include <math.h> #include <time.h> int expmong (int p, int ak); int main() { double pid, s1, s2, s3, s4; double series (int m, int n); void ihex (double x, int m, char c[]); int id = 1000000; #define NHX 16 char chx[NHX]; clock_t start,end; /* id is the digit position. Digits generated follow immediately after id. */ start = clock(); s1 = series (1, id); s2 = series (4, id); s3 = series (5, id); s4 = series (6, id); pid = 4. * s1 - 2. * s2 - s3 - s4; pid = pid - (int) pid + 1.; ihex (pid, NHX, chx); end = clock(); printf (" position = %i\n fraction = %.15f \n hex digits = %10.10s\n time = %.3f[sec]", id, pid, chx, (double)(end-start)/CLOCKS_PER_SEC); return 0; } void ihex (double x, int nhx, char chx[]) /* This returns, in chx, the first nhx hex digits of the fraction of x. */ { int i; double y; char hx[] = "0123456789ABCDEF"; y = fabs (x); for (i = 0; i < nhx; i++){ y = 16. * (y - floor (y)); chx[i] = hx[(int) y]; } } #define eps 1e-17 double series (int m, int id) /* This routine evaluates the series sum_k 16^(id-k)/(8*k+m) using the modular exponentiation technique. */ { int k, ak, p; double s, t; s = 0.; /* Sum the series up to id. */ if (m == 4){ for (k = 0; k < id; k++){ ak = 2 * k + 1; p = expmong (id - k - 1, ak); t = (p * (4 % ak)) % ak; s = s + t / ak; s = s - (int) s; } }else if (m == 6){ for (k = 0; k < id; k++){ ak = 4 * k + 3; p = expmong (id - k - 1, ak); t = (p * (8 % ak)) % ak; s = s + t / ak; s = s - (int) s; } }else{ for (k = 0; k < id; k++){ ak = 8 * k + m; t = expmong (id - k, ak); s = s + t / ak; s = s - (int) s; } } /* Compute a few terms where k >= id. */ for (k = id; k <= id + 100; k++){ ak = 8 * k + m; t = pow (16., (double) (id - k)) / ak; if (t < eps) break; s = s + t; s = s - (int) s; } return s; } // tのモンゴメリリダクション int reduction(__int64 t, int n, int n2, int nb) { static int masktbl[] = { 0, 0x00000001,0x00000003,0x00000007,0x0000000f,0x0000001f,0x0000003f,0x0000007f,0x000000ff, 0x000001ff,0x000003ff,0x000007ff,0x00000fff,0x00001fff,0x00003fff,0x00007fff,0x0000ffff, 0x0001ffff,0x0003ffff,0x0007ffff,0x000fffff,0x001fffff,0x003fffff,0x007fffff,0x00ffffff, 0x01ffffff,0x03ffffff,0x07ffffff,0x0fffffff,0x1fffffff,0x3fffffff,0x7fffffff,0xffffffff, }; __int64 c = t * n2; c &= masktbl[nb]; // mod Rの意味,(nb)bit以上を0クリア c = c * n + t; c >>= nb; // 1/r の意味 if (c >= n) c -= n; return c; } // モンゴメリ冪剰余計算 int expmong (int p, int ak) { /* expm = 16^p mod ak. */ int nb = 0; // 有効Bit数 int r; // r: nより大きな2のべき for (nb=0, r=1; r<ak; nb++, r<<=1) ; // r2 = r^2 mod ak int r2 = ((__int64)r * r) % ak; // n*n2 ≡ -1 mod r int n2 = 0; /* 求めるN' */ { int t=0, vi=1, ni=nb; while (ni--){ if ((t & 1) == 0){ t += ak; n2 += vi; } t >>= 1; vi <<= 1; } } // 冪剰余 16^p mod ak, バイナリ法の下位桁から計算 int q = reduction(16 * r2, ak, n2, nb); int x = reduction(r2, ak, n2, nb); while (p > 0){ if (p & 1){ x = reduction((__int64)x * q, ak, n2, nb); } q = reduction((__int64)q * q, ak, n2, nb); p >>= 1; } return reduction(x, ak, n2, nb); }
改変は、series() のm=4,m=6の処理とexpm()→expmong()です。
intel系x86コードでの64bit整数演算は早くないので、面白い結果が出ました。
BBP計算速度テスト (x86用,x64用ターゲットを変えてBuildしている)
【右向きバイナリ法(WindowsXP 32bit)】
(1回目)
position = 1000000
fraction = 0.423429797567895
hex digits = 6C65E52CB4
time = 2.763[sec]
(2回目)
position = 1000000
fraction = 0.423429797567895
hex digits = 6C65E52CB4
time = 2.804[sec]
(3回目)
position = 1000000
fraction = 0.423429797567895
hex digits = 6C65E52CB4
time = 2.763[sec]
【モンゴメリ法(WindowsXP 32bit)】
(1回目)
position = 1000000
fraction = 0.423429797567801
hex digits = 6C65E52CB4
time = 3.114[sec]
(2回目)
position = 1000000
fraction = 0.423429797567801
hex digits = 6C65E52CB4
time = 3.134[sec]
(3回目)
position = 1000000
fraction = 0.423429797567801
hex digits = 6C65E52CB4
time = 3.204[sec]
【結果】
およそ15%、モンゴメリ法が時間が掛る
【右向きバイナリ法(Windows7 64bit)】
(1回目)
position = 1000000
fraction = 0.423429797567895
hex digits = 6C65E52CB4
time = 1.788[sec]
(2回目)
position = 1000000
fraction = 0.423429797567895
hex digits = 6C65E52CB4
time = 1.801[sec]
(3回目)
position = 1000000
fraction = 0.423429797567895
hex digits = 6C65E52CB4
time = 1.786[sec]
【モンゴメリ法(Windows7 64bit)】
(1回目)
position = 1000000
fraction = 0.423429797567895
hex digits = 6C65E52CB4
time = 1.255[sec]
(2回目)
position = 1000000
fraction = 0.423429797567895
hex digits = 6C65E52CB4
time = 1.258[sec]
(3回目)
position = 1000000
fraction = 0.423429797567895
hex digits = 6C65E52CB4
time = 1.223[sec]
【結果】
およそ30%、モンゴメリ法が早い
VC2010でBuildした限りでは、
32bitではバイナリ法の方が早く、64bitではモンゴメリ法の方が早くなりました。
バイナリ法のコードも整数演算化してみたのですが、
部分的なコード変更だと、かえって成績が悪くなってしまいました。
バイナリ法のコンパイラオプションでSSE2を有効にしてみてもあまり効果はなかったのですが、
Intelコンパイラを使うと、もう少し早くなるかもしれません。
このコードでも、2〜3千万桁までは計算できますが、
expmong()の変数 r2 と series()の変数 p の型を__int64にすれば、1億桁まで計算できるようになります。
但し、x86(32bit)だと64bit整数演算が増えるとそれだけ処理が遅くなります。
x64で1億桁の計算は、私のPCでは150秒ほどでした。
拡張倍精度(仮数部64bit)と長整数(80bit程度)を組み合わせれば、このアルゴリズムでも100億桁ぐらいは行けると思いますが、これだけの計算量になると普通のPCでは難しいです。(電気代も上がるし...)
Tags: プログラムメモ
author : HUNDREDSOFT | - | -