ニュートン法を使った2進多桁の整数平方根(その2)
| プログラムメモ | 2011/02/06 Sun 10:27
前回、平方根 √s をNewton法を使って解くプログラムを紹介しましたが、
単独の初期値を使った方法では、あまり早くありません。
数万bitを超える多桁演算の場合、64bit精度の初期値を使ったとしても、あまり速度に差が出ません。
そこで大きな桁(数万bitを超える)で計算を開始するのではなく、(s)の先頭部分を使った小さな桁で計算を開始して、これをNewton法の初期値とし、もう少し大きな桁でNewton法を解く、
これを繰り返して最終的な答えを得る方法を紹介します。
newtonsqrtは、Newton法で (2n / √q) を求める関数です。
初回は先頭64bit程度で計算します。
2回目は、初回の計算結果を初期値として、(n/8)桁増やして計算。
3回目は、2回目の計算結果を初期値として、更に(n/8)桁増やして計算。
と次々と桁を増やしていきます。
計算時間は明らかに短くなります。
この方法は、Bigintの演算回数としては、効果はないのですが、
可変長のFFT乗算を用いる場合、演算量は2の冪数桁単位に増加するので、
Totalの計算量としては、こちらの方が有利です。
分割数は、利用するBigint(多倍長整数)クラスで最速の性能が出るように調節する必要があります。
これについては、「高橋 大介, 金田 康正. "多倍長平方根の高速計算法". 情報処理学会研究報告 95-HPC-58, pp.51-56.」が詳しいです。
文献に従えば、初期値に倍精度結果を使う・3〜4分割程度・FFT再利用、を行えば最大限の高速化を望めますが、このサンプルコードではそこまで対応できていません。
また、この方法は平方根に限らず、Newton法を使った様々な計算に応用できます。
整数平方根での詳細解説
整数除算での詳細解説
このアルゴリズムを利用した16進・2進・10進電卓です。
整数だけですがおよそ100万桁まで計算できます。

(注)ここでのBigintクラスは、多倍長整数を格納する仮想のクラスであり、実在するものではありません。
Tags: プログラムメモ
単独の初期値を使った方法では、あまり早くありません。
数万bitを超える多桁演算の場合、64bit精度の初期値を使ったとしても、あまり速度に差が出ません。
そこで大きな桁(数万bitを超える)で計算を開始するのではなく、(s)の先頭部分を使った小さな桁で計算を開始して、これをNewton法の初期値とし、もう少し大きな桁でNewton法を解く、
これを繰り返して最終的な答えを得る方法を紹介します。
Bigint newtonsqrt(const Bigint& q, const int& n, const Bigint& init){ Bigint x(init), m(0), c3(3); c3 <<= n; while(m != x){ m = x; x *= c3 - ((m * m * q) >> n); x >>= n+1; } return x; } Bigint iSqrt(Bigint s){ int n = s.length(); // bit数 int b; if (n & 1) b = 65; // 初期演算Bit数(n:奇数) else b = 64; // 初期演算Bit数(n:偶数) Bigint x = 1; x <<= (b / 2); // Newton法の初期値として, 1 << (b/2) を与える。 Bigint w; int m = n / 8; // 4分割程度 while(1){ w = s >> (n - b); // (s)先頭から指定bit数(n-b)切り取り x = newtonsqrt(w, b, x); if (b + 2 * m > n) break; b += 2 * m; x <<= m; } x <<= (n - b) / 2; // 必ず割り切れる x = newtonsqrt(s, n, x); x *= s; // x = s * (2^n) / √s = (2^n) * √s x >>= n; // x = √s // 誤差修正 w = x + 1; if (s >= w * w){ x = w; } return x; }
newtonsqrtは、Newton法で (2n / √q) を求める関数です。
初回は先頭64bit程度で計算します。
2回目は、初回の計算結果を初期値として、(n/8)桁増やして計算。
3回目は、2回目の計算結果を初期値として、更に(n/8)桁増やして計算。
と次々と桁を増やしていきます。
計算時間は明らかに短くなります。
この方法は、Bigintの演算回数としては、効果はないのですが、
可変長のFFT乗算を用いる場合、演算量は2の冪数桁単位に増加するので、
Totalの計算量としては、こちらの方が有利です。
分割数は、利用するBigint(多倍長整数)クラスで最速の性能が出るように調節する必要があります。
これについては、「高橋 大介, 金田 康正. "多倍長平方根の高速計算法". 情報処理学会研究報告 95-HPC-58, pp.51-56.」が詳しいです。
文献に従えば、初期値に倍精度結果を使う・3〜4分割程度・FFT再利用、を行えば最大限の高速化を望めますが、このサンプルコードではそこまで対応できていません。
また、この方法は平方根に限らず、Newton法を使った様々な計算に応用できます。
整数平方根での詳細解説
整数除算での詳細解説
このアルゴリズムを利用した16進・2進・10進電卓です。
整数だけですがおよそ100万桁まで計算できます。
(注)ここでのBigintクラスは、多倍長整数を格納する仮想のクラスであり、実在するものではありません。
Tags: プログラムメモ
多桁の整数値(S)の平方根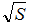 があったとして、 があったとして、 |
| Newton法(2次漸化式)を用いて平方根の整数部分を求める方法を考える。 |
扱う桁数や除算の速度によっては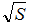 を直接求めてもよいが、 を直接求めてもよいが、 |
ここでは整数(S)の有効bit数を (b) として、まず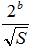 を求め、 を求め、 |
しかる後に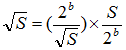 を解いて平方根を求める。 を解いて平方根を求める。 |
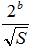 の漸化式は次のように表せる。 の漸化式は次のように表せる。 |
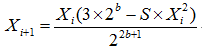 |
| Newton法を使って(n)回の繰り返しにより、整数桁数分の精度が得られたとすれば、整数平方根は、 |
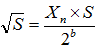 |
| となる。具体的なコード例は、newtonsqrt()を参照のこと。 |
Newton法の計算では、初期値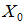 の工夫によりループ回数が削減できる。 の工夫によりループ回数が削減できる。 |
| 例えば、10進で300桁以下の小さな整数であれば、多倍長整数を倍精度小数点数(double)に 変換して、標準ライブラリのsqrt()を呼び出せば良い。 5000桁以下であれば拡張倍精度小数点数で演算できるが、VCではアセンブラが必要になる。 |
| もっと大きな桁の場合、多倍長整数(S)の上位bitを取り出して浮動小数点演算を行う。 |
| (S) の上位bit部分を (S') として次式が成り立つように(m)をとる。 |
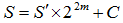 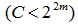 |
| ここでは初期値となる近似値を求めたいので、(C) を無視すると |
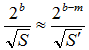 |
従って、(S') を浮動小数点形式で表現可能な範囲に取れば、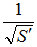 は標準ライブラリで計算できる。 は標準ライブラリで計算できる。 |
ところで浮動小数点で計算すると、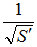 は整数部を持たない。 は整数部を持たない。 |
整数部で53bit(倍精度),64bit(拡張倍精度)の精度を持つように、適当な大きさの 2の冪数 (2p) を掛ける。その後、浮動小数点形式から多倍長整数に戻し、多倍長整数に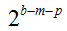 |
| を掛ければ良い。 |
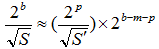 |
実際には浮動小数点数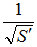 の仮数部をそのまま多倍長整数に入れ、指数部にわずかな操作(加減算)を加えてシフト演算するだけである。 の仮数部をそのまま多倍長整数に入れ、指数部にわずかな操作(加減算)を加えてシフト演算するだけである。 |
| Newton法の初期値算出にNewton法を使う | |
|
FFT乗算を用いた多桁演算に於いては、初期値を一度だけ与えて、 Newton法を用いるのは効率的ではない。 | |
| 徐々に計算桁数を増加させて、Newton法を繰り返す方法が一般に用いられる。 | |
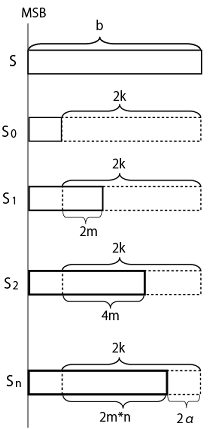 |
b[bit]の2進数(S)を考え、 このとき 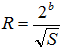 を求めるものとする。 を求めるものとする。S に適当な初期値を与え、 その上位bit部分をS0とすれば、 その時の初期値R0は前出の初期値算出を使って次式で表せる。 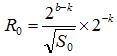 次に計算幅を(2m)広げてS1の範囲で Newton法を行うとすれば、初期値R1は 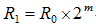 R1を使って得られるNewton法の解をR'1とすれば初期値R2は 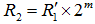 以降(n-1)回繰り返して、2α[bit]残った場合は 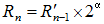 を初期値として、 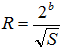 を求めれば良い。 を求めれば良い。 |
| 具体的なコード例は、iSqrt()のwhile loop 付近を参照のこと。 | |
author : HUNDREDSOFT | - | -